Counting contra dances
From a talk given for the
Mathematical Association of America
January, 2003
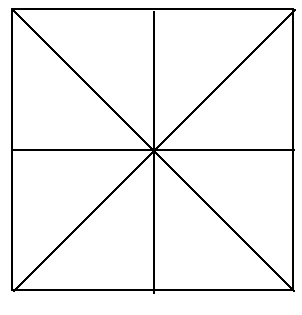
At the 2003 annual meeting of the National Council of Teachers of Mathematics (NCTM), I'll be presenting a session on the mathematics of contra dance. We'll do some dancing and then literally walk through the generation of the symmetries from two figures. To accomplish this, I wanted a dance that illustrated all eight symmetries of a square.
At first this seemed reasonable, since most contra dances consist of 7-9 figures (each taking 4, 8, or 12 beats of music, for a total of 64 beats).

On second thought, though, there could be no dance that was a sequence of the eight elements of D4, because these elements include 4 reflections, whose product will not change the orientation of the square. And the dance sequence must result in a reflection, because the two couples change places.
So, on third thought, I decided to look for a dance that had no figures representing the identity element but had a duplicate reflection. In fact, many contra dances include two swings—one between partners and one between neighbors—so repeating this one reflection was reasonable.
But I couldn't find any dance that satisfied these criteria. So I tried a time-honored method of finding out why something is impossible: I tried to do it. And, with much effort, I did in fact write a dance. Unfortunately, the dance was terrible; the dancers were required to move awkwardly between figures.
Because the writing process had been so difficult, I didn't try to adjust the result. Instead, I considered writing a computer program to generate all dances satisfying my criteria.
But that idea lead to the problem that led to the group theory: Would the output be so voluminous that scanning it for smooth dances would be more time consuming than writing a new dance?
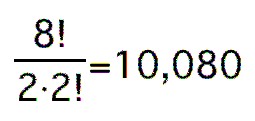
You might think that, yes, there are 8! arrangements of the 8 figures, and that's a lot. Even if we have two swings, and if only half the dances end with the couples interchanged, that's still too much output to sift through. But I'd learned a few things in writing my dance.
First, three of the dance figures I wanted to use can take place only if the lady is to the right of the gent. What does this mean in terms of D4? Those three figures correspond to reflections through the diagonals of the square and a rotation of the square through 180 degrees. Now you may notice that these three elements, along with the identity element we're ignoring, form of subgroup of D4. Let's call the subgroup K.
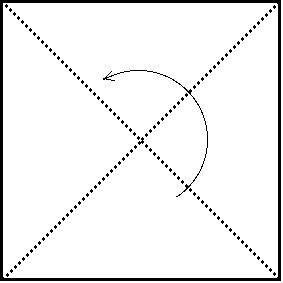
The condition that the figures representing the elements of K can occur only when the lady is to the right of the gent is equivalent to saying that the product of the elements of the sequence must be not in K when an element of K occurs in the sequence.
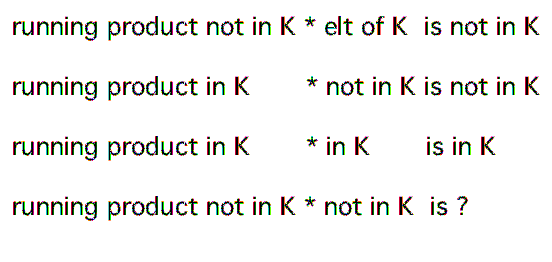
That observation got me thinking about how the running product moves in and out of K. If the running product is an element of K, or if an element of K is applied, then we know a lot, because K is a subgroup. But what if neither the running product nor the next element is an element of this subgroup? In most cases, we can't say much about the product of two elements of a group that aren't in a given subgroup.
But K is a special subgroup, because it's half of D4. It's a normal subgroup, so the operation on its two cosets is well-defined. It follows that, if the running product is not in K, and an element not in K is applied, then the result will be in K.
The fact that the quotient group is isomorphic to Z2 gives us some convenient notation.
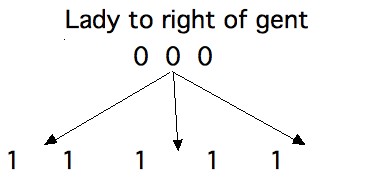
Let's represent the elements of K by 0s and the other elements by 1s. Because we've substituted an extra swing (a 1) for the identity element (a 0), we have 3 0s and 5 1s. The fact that the 0s must occur when the running product is not in K means that they must appear in the sequence after an odd number of 1s. That is, they must go after the first, third, or fifth 1. They might be all together or spread apart. Elementary combinatorics shows that there are 60 ways of fitting in the 0s.
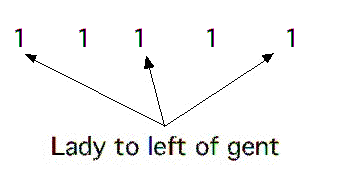
Group theory helped make use of a second observation in writing a dance: There are two figures that can happen only if the lady is to the left of the gent. These special figures are not in K, so they are represented by the first, third, and fifth 1s. In fact, two of the three figures are the swings, and there are only 3 ways to choose two of 1s to represent the swings. With the two possibilities for the other two 1s, we have 360 possible dances satisfying the criteria.
Indeed, I wrote the computer program. Most of the 360 possibilities could be eliminated on aesthetic grounds. I was left with about 12 dance sequences. My personal preferences cut them down to 4 dances, one of which I have chosen as the dance for the April NCTM session. Thanks go to dancers and a caller at Tapestry Folkdance Center in Minneapolis for helping to test and improve this dance..
Last update 15-Dec-2004